A bond payable is just a promise to pay a series of payments over time (the interest component) and a fixed amount at maturity (the face amount). Thus, it is a blend of an annuity (the interest) and lump sum payment (the face). To determine the amount an investor will pay for a bond, therefore, requires present value computations to determine the current worth of the future payments. Assume that Schultz Company issues 5-year, 8% bonds. Bonds frequently have a $1,000 face value and pay interest every six months. Using these assumptions, consider the following three alternative scenarios:



The following table shows calculations of the price of the bond under different scenarios:
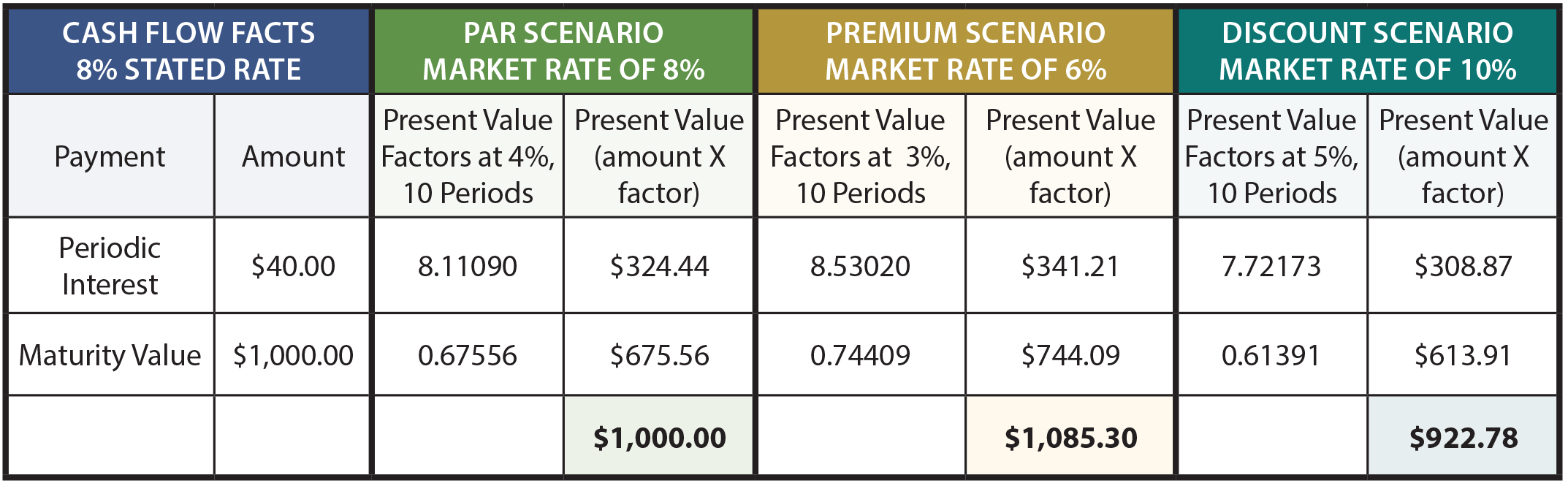
To further explain, the interest amount on the $1,000, 8% bond is $40 every six months. Because the bonds have a 5-year life, there are 10 interest payments (or periods). The periodic interest is an annuity with a 10-period duration, while the maturity value is a lump-sum payment at the end of the tenth period. The 8% market rate of interest equates to a semiannual rate of 4%, the 6% market rate scenario equates to a 3% semiannual rate, and the 10% rate is 5% per semiannual period.
The present value factors are taken from the present value tables (annuity and lump-sum, respectively). Take time to verify the factors by reference to the appropriate tables, spreadsheet, or calculator routine. The present value factors are multiplied by the payment amounts, and the sum of the present value of the components would equal the price of the bond under each of the three scenarios.
Note that the 8% market rate assumption produced a bond priced at $1,000, the 6% assumption produced a bond priced at $1,085.30 (which includes an $85.30 premium), and the 10% assumption produced a bond priced at $922.78 (which includes a $77.22 discount).
These calculations are not only correct theoretically, but are very accurate financial tools. However, one point is noteworthy. Bond pricing is frequently to the nearest 1/32nd. That is, a bond might trade at 103.08. One could easily misinterpret this price as $1,030.80. But, it actually means 103 and 8/32. In dollars, this would amount to $1,032.50 ($1,000 X 103.25). Having learned the financial mechanics of bonds, it is now time to examine the correct accounting.
Bonds Issued At Par
If Schultz issued 100 of its 5-year, 8% bonds at par, the following entries would be required :

Bonds Issued At A Premium
One simple way to understand bonds issued at a premium is to view the accounting relative to counting money! If Schultz issues 100 of the 8%, 5-year bonds when the market rate of interest is only 6%, then the cash received is $108,530 (see the previous calculations). Schultz will have to repay a total of $140,000 ($4,000 every 6 months for 5 years, plus $100,000 at maturity).
Thus, Schultz will repay $31,470 more than was borrowed ($140,000 – $108,530). This $31,470 must be expensed over the life of the bond; uniformly spreading the $31,470 over 10 six-month periods produces periodic interest expense of $3,147 (not to be confused with the actual periodic cash payment of $4,000).
Another way to illustrate this problem is to note that total borrowing cost is reduced by the $8,530 premium, since less is to be repaid at maturity than was borrowed up front. Therefore, the $4,000 periodic interest payment is reduced by $853 of premium amortization each period ($8,530 premium amortized on a straight-line basis over the 10 periods), also producing the periodic interest expense of $3,147 ($4,000 – $853).
This topic is inherently confusing, and the journal entries are actually clarifying. Notice that the premium on bonds payable is carried in a separate account (unlike accounting for investments in bonds covered in a prior chapter, where the premium was simply included with the Investment in Bonds account).

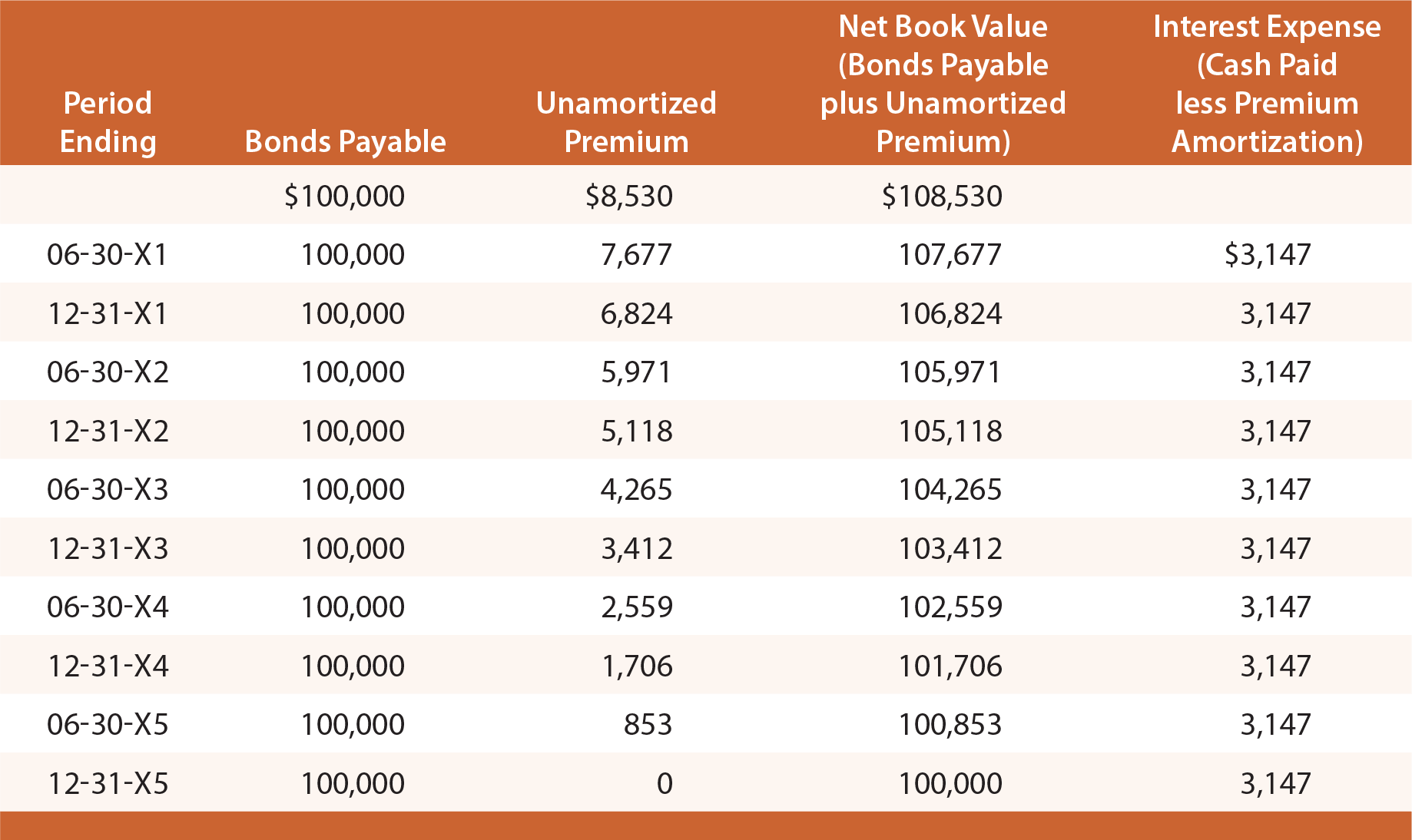
Study the following illustration, and observe that the Premium on Bonds Payable is established at $8,530, then reduced by $853 every interest date, bringing the final balance to zero at maturity.
On any given financial statement date, Bonds Payable is reported on the balance sheet as a liability, along with the unamortized Premium balance (known as an “adjunct” account). To illustrate, the balance sheet disclosures would appear as follows on December 31, 20X3 and 20X4:


The income statement for all of 20X3 would include $6,294 of interest expense ($3,147 X 2). This method of accounting for bonds is known as the straight-line amortization method, as interest expense is recognized uniformly over the life of the bond. Although simple, it does have one conceptual shortcoming. Notice that interest expense is the same each year, even though the net book value of the bond (bond plus remaining premium) is declining each year due to amortization.
As a result, interest expense each year is not exactly equal to the effective rate of interest (6%) that was implicit in the pricing of the bonds. For 20X1, interest expense can be seen to be roughly 5.8% of the bond liability ($6,294 expense divided by beginning of year liability of $108,530). For 20X4, interest expense is roughly 6.1% ($6,294 expense divided by beginning of year liability of $103,412).
Accountants have devised a more precise approach to account for bond issues called the effective-interest method. Be aware that the more theoretically correct effective-interest method is actually the required method, except in those cases where the straight-line results do not differ materially. Effective-interest techniques are introduced in a following section of this chapter.
Bonds Issued At A Discount
If Schultz issues 100 of the 8%, 5-year bonds for $92,278 (when the market rate of interest is 10%), Schultz will still have to repay a total of $140,000 ($4,000 every 6 months for 5 years, plus $100,000 at maturity). Thus, Schultz will repay $47,722 ($140,000 – $92,278) more than was borrowed. Spreading the $47,722 over 10 six-month periods produces periodic interest expense of $4,772.20 (not to be confused with the periodic cash payment of $4,000).
Another way to consider this problem is to note that the total borrowing cost is increased by the $7,722 discount, since more is to be repaid at maturity than was borrowed initially. Therefore, the $4,000 periodic interest payment is increased by $772.20 of discount amortization each period ($7,722 discount amortized on a straight-line basis over the 10 periods), producing periodic interest expense that totals $4,772.20.
Like bond premiums, discounts are also carried in a separate account. The following entry is needed to record the initial bond issuance:

The following entries reflect periodic interest and repayment at maturity:

Carefully study this illustration, and observe that the Discount on Bonds Payable is established at $7,722, then reduced by $772.20 on every interest date, bringing the final balance to zero at maturity. On any given financial statement date, Bonds Payable is reported on the balance sheet as a liability, along with the unamortized Discount that is subtracted (known as a “contra” account). The illustration below shows the balance sheet disclosure as of June 30, 20X3. Note that the unamortized discount on this date is determined by calculations revealed in the table that follows:

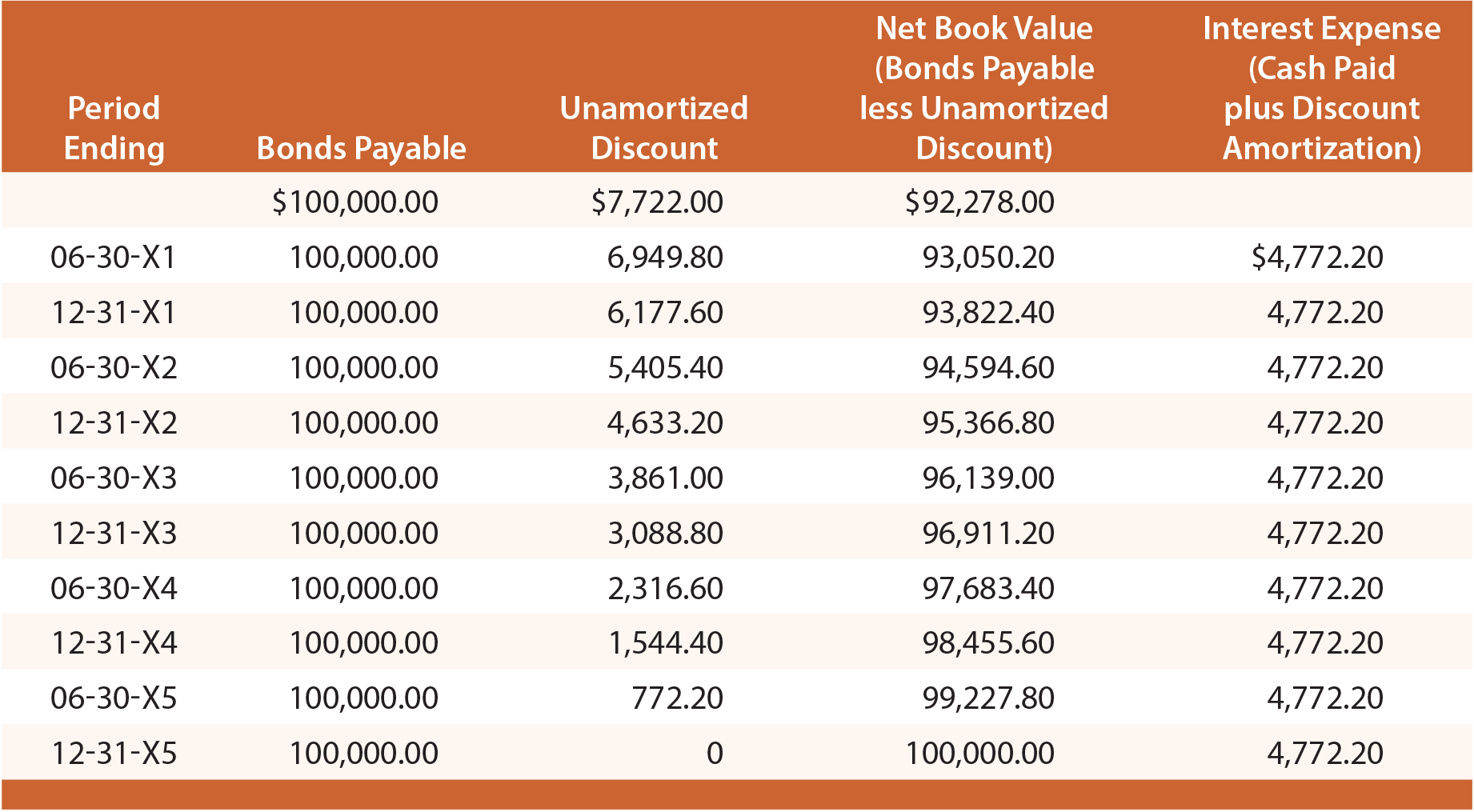
Each yearly income statement would include $9,544.40 of interest expense ($4,772.20 X 2). The straight-line approach suffers from the same limitations discussed earlier, and is acceptable only if the results are not materially different from those resulting with the effective-interest technique.
| Did you learn? |
|---|
| What factors will generally impact the issue price of a bond? |
| Understand why present value is important to bond pricing calculations. |
| Be able to calculate the issue price for a bond. |
| Prepare journal entries for the entire life cycle of a bond issued at par. |
| Be able to describe when a bond is issued at a premium, and prepare journal entries for its issuance. |
| Use the straight-line method to account for a bond issued at a premium. |
| Be able to describe when a bond is issued at a discount, and prepare journal entries for its issuance. |
| Use the straight-line method to account for a bond issued at a discount. |
| Understand how bonds are presented on a balance sheet, whether issued at par, a premium, or discount. |
