There is an expression that “time is money.” In capital budgeting, this concept is actually measured and brought to bear on the decision process. The fundamental idea is that a dollar received today is worth more than a dollar to be received in the future. This result occurs because a dollar in hand today can be invested to generate additional immediate returns.
In the context of capital budgeting, assume two alternative investments have the same upfront cost. Investment Alpha returns $100 per year for each of the next 5 years. Investment Beta returns $50 per year for each of the next 10 years. Based solely on this information, one should conclude that Alpha is preferred to Beta. Although the total cash returns are the same, the time value of money is better for Alpha than Beta. With Alpha, the money is returned sooner, allowing for enhanced reinvestment opportunities. Of course, very few capital expenditure choices are as clear cut as Alpha and Beta. Therefore, accountants rely on precise mathematical techniques to quantify the time value of money.
Compound Interest
The starting point for understanding the time value of money is to develop an appreciation for compound interest. Albert Einstein is quoted as saying: “The most powerful force in the universe is compound interest.” Very simply, money can be invested to earn money.
In this context, consider that when one spends a dollar on a soft drink, that person is actually foregoing $0.10 per year for the rest of their life (assuming a 10% interest rate). And, as will be shown, that annual dime of savings builds to much more because of interest that is earned on the interest.
Compound interest calculations can be used to compute the amount to which an investment will grow in the future. Compound interest is also called future value. If one invests $1 for one year, at 10% interest per year, how much will he or she have at the end of the year? The answer, of course, is $1.10. This is calculated by multiplying the $1 by 10% ($1 X 10% = $0.10) and adding the $0.10 to the initial dollar. If the resulting $1.10 is invested for another year at 10%, it will grow to $1.21. That is, $1.10 X 110%. This process will continue, year after year.
The annual interest each year is larger than the year before because of “compounding.” Compounding simply means that an investment is growing with accumulated interest and earning interest on previously accrued interest that becomes part of the total investment pool. This formula expresses the basic mathematics of compound interest:
(1+i)n
Where “i” is the interest rate per period and “n” is the number of periods
Future Value Of Lump Sum
How much would $1 grow to in 25 years at 10% interest? The answer can be determined by taking 1.10 to the 25th power [(1.10)25], and the answer is $10.83. Future value tables provide predetermined values for a variety of such computations (see the companion website for a complete set of tables). To experiment with a future value table, determine how much $1 would grow to in 10 periods at 5% per period. The answer to this question is $1.63 and can be found by reference to the value in the “5% column/10-period row.” If the original investment was $5,000 (instead of $1), the investment would grow to $8,144.45 ($5,000 X 1.62889).
In using the tables, be sure to note that the interest rate is the rate per period. The “period” might be years, quarters, months, etc. It all depends on how frequently interest is to be compounded. For instance, a 12% annual interest rate, with monthly compounding for two years, would require reference to the 1% column (12% annual rate equates to a monthly rate of 1%) and 24-period row (2 years equates to 24 months). If the same investment involved annual compounding, then one would refer to the 12% column and 2-period row. The frequency of compounding makes a difference in the amount accumulated. For the given example, monthly compounding returns 1.26973, while annual compounding returns only 1.25440.
Future Value Of Annuities
Annuities are level streams of payments. Each payment is the same amount and occurs at a regular interval. Annuities are common in business. They can arise in loans, retirement plans, leases, insurance settlements, tax-related calculations, and so forth. Sometimes, one may be curious to learn how much a recurring stream of payments will grow to after a number of periods. This is called the future value of an annuity.
Annuity Due
An annuity due (also known as an annuity in advance) involves a level stream of payments, with the payments being made at the beginning of each time period. For instance, perhaps one plans on saving for retirement by investing $5,000 at the beginning of each year for the next five years. If the annual interest rate is 10% per year, how much will accumulate by the end of the 5-year period? The following graphic shows how each of the five individual payments would grow, and the accumulated total would reach $33,578:
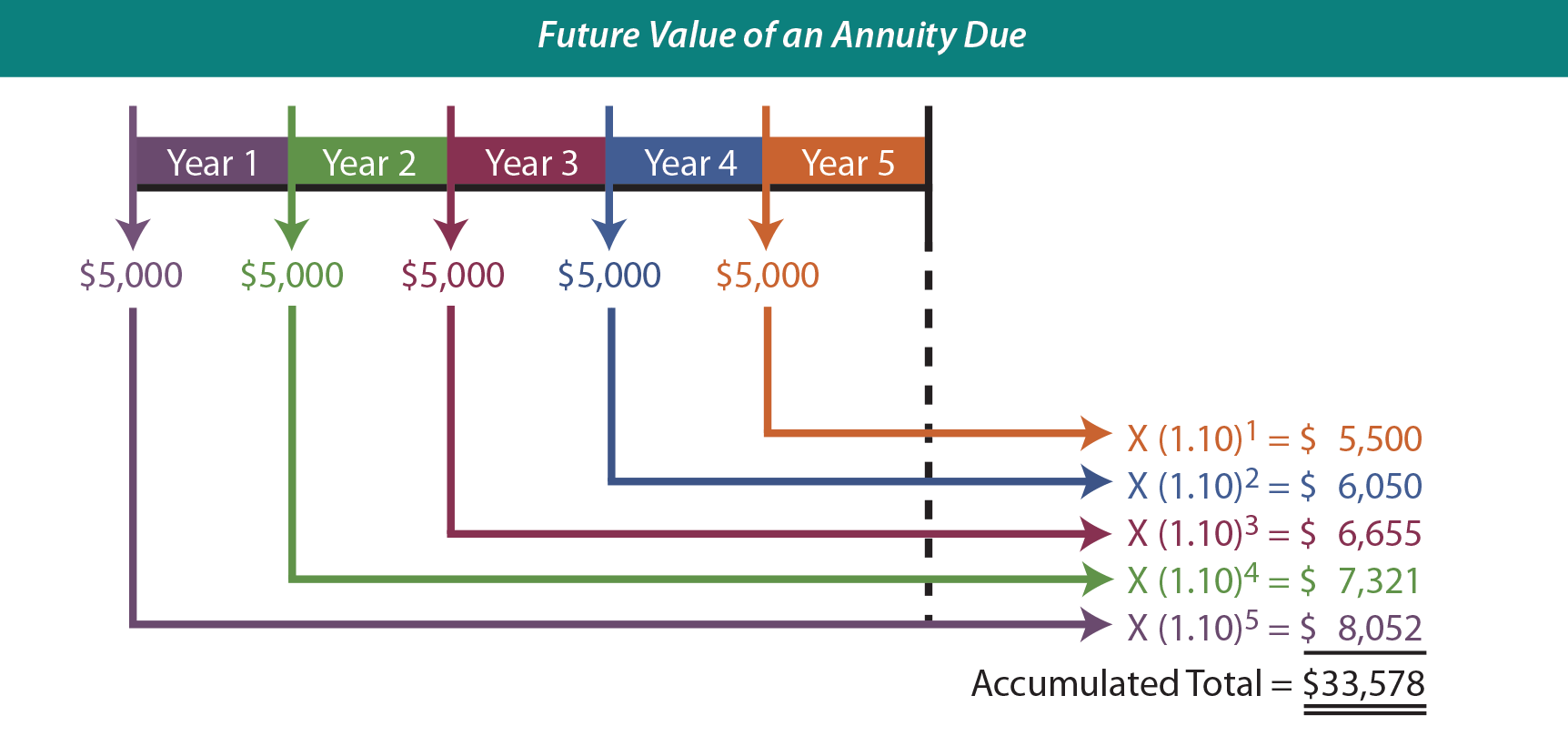
Although the graphic provides a useful explanatory tool, it is a bit cumbersome to implement. The same conclusion can be reached by reference to a future value of an annuity due table. The table reveals a value of 6.71561 (10% column/5-period row). Multiplying the $5,000 annual payment by this factor yields $33,578 ($5,000 X 6.71561). This means that the annuity will grow to $33,578.
Ordinary Annuity
Sometimes an annuity will be based on “end of period” payments. These annuities are called ordinary annuities (also known as annuities in arrears). The next graphic portrays a 5-year, 10%, ordinary annuity involving level payments of $5,000 each.
Notice the similarity to the preceding graphic, except that each year’s payment is shifted to the end of the year. This means that each payment will accumulate interest for one less year, and the final payment will accumulate no interest! Be sure to note the striking difference between the accumulated total under an annuity due versus an ordinary annuity ($33,578 vs. $30,526).
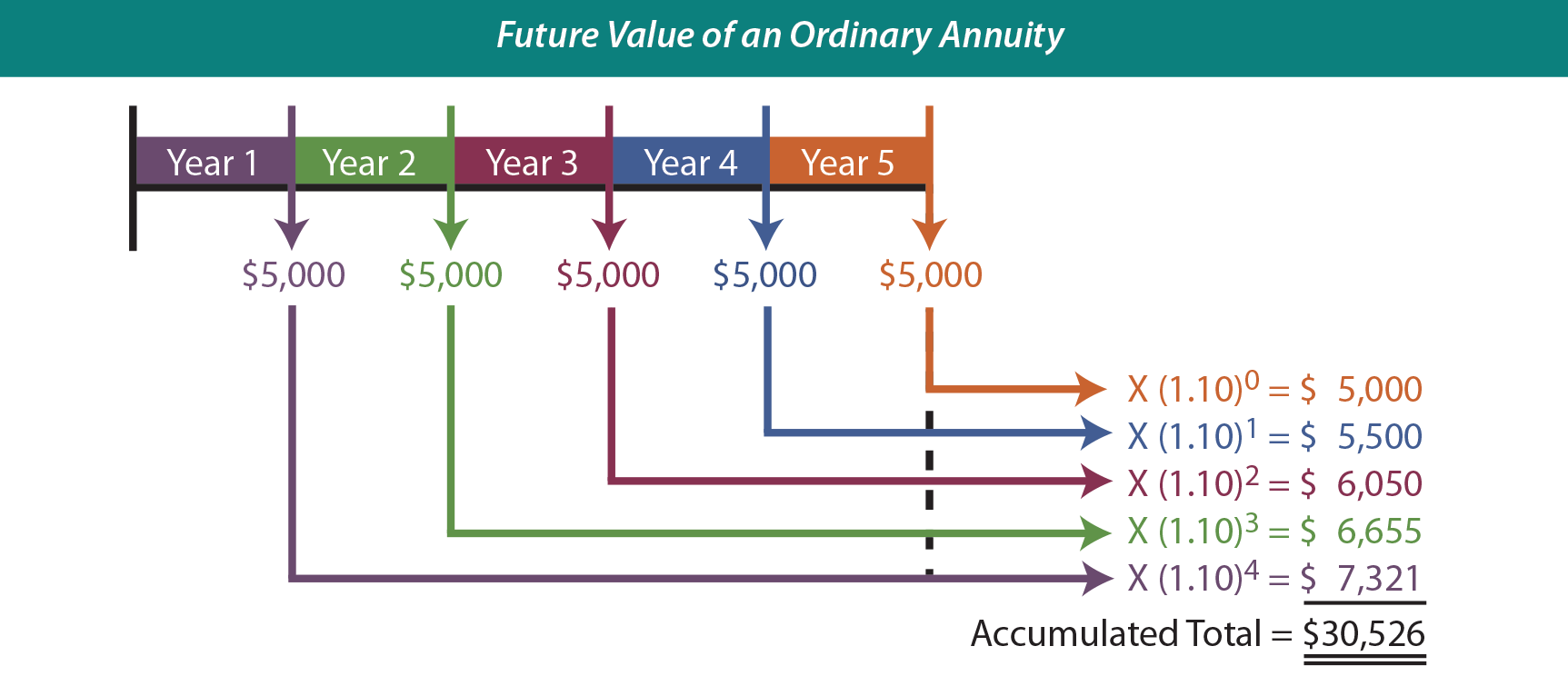
There are also tables that reflect the future value of an ordinary annuity. Review a table to become satisfied about the $30,526 amount ($5,000 X 6.10510).
Present Value
Future value calculations provide useful tools for financial planning. But, many decisions and accounting measurements will be based on a reciprocal concept known as present value. Present value (also known as discounting) determines the current worth of cash to be received in the future.
For instance, how much would one be willing to take today, in lieu of $1 in one year? If the interest rate is 10%, presumably he or she would accept the sum that would grow to $1 in one year if it were invested at 10%. This happens to be $0.90909. In other words, invest 90.9¢ for a year at 10%, and it will grow to $1 ($0.90909 X 1.1 = $1). Thus, present value calculations are simply the reciprocal of future value calculations. In formula terms this would be 1/(1+i)n.
A present value of $1 table reveals predetermined values for calculating the present value of $1, based on alternative assumptions about interest rates and time periods. A $25,000 lump sum amount to be received at the end of 10 years, at 8% annual interest, with semiannual compounding, would have a present value of $11,410 (recall the earlier discussion, and use the 4% column/20-period row: $25,000 X 0.45639).
Annuity Due
Present value calculations are applicable to annuities also. Perhaps one is considering buying an investment that returns $5,000 per year for five years, with the first payment to be received immediately. What should be paid for this investment if the target rate of return is 10%? This scenario relates to the present value of an annuity due:
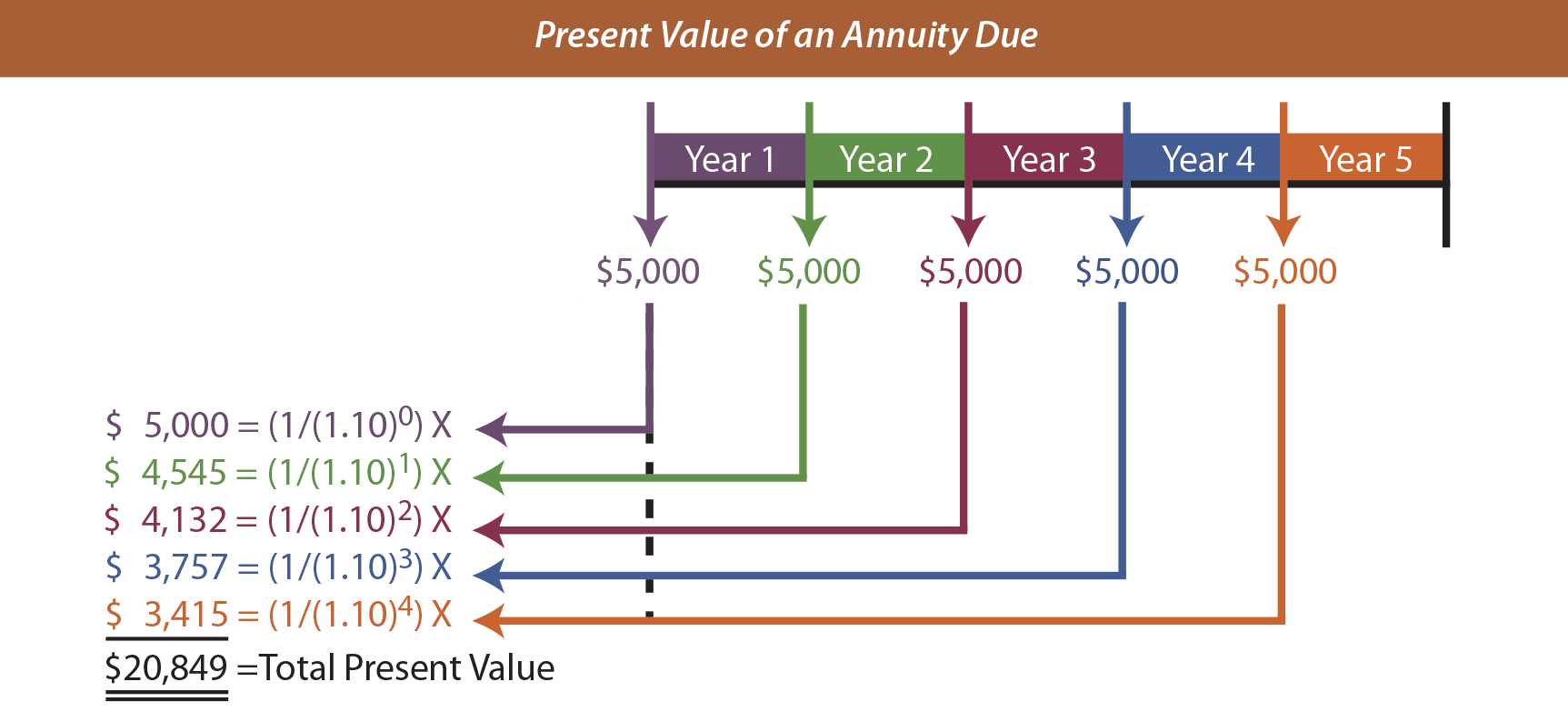
The graphic shows that the annuity has a present value of $20,849. Of course, there is a present value of an annuity due table to ease the burden of this calculation ($5,000 X 4.16897 = $20,849).
Ordinary Annuity
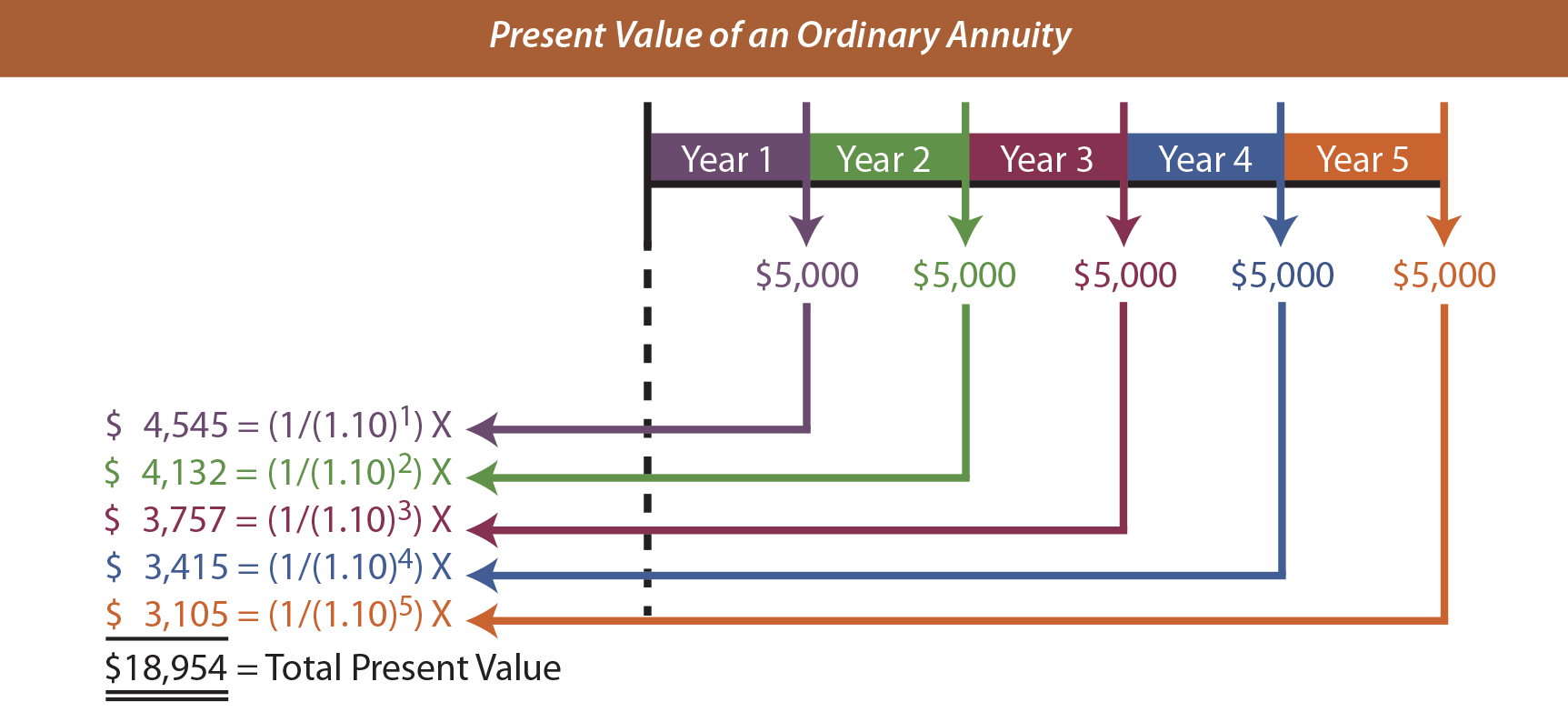
Many times, the first payment in an annuity occurs at the end of each period. The present value of an ordinary annuity table provides the necessary factor to determine that $5,000 to be received at the end of each year for a 5-year period is worth only $18,954, assuming a 10% interest rate ($5,000 X 3.79079 = $18,954). The following graphic confirms this conclusion:
Electronic Spreadsheet
Be aware that most electronic spreadsheets also include functions for calculating present and future value amounts by simply completing a set of predetermined queries.
These spreadsheet functions can prove to be very efficient and effective in performing the calculations illustrated in this chapter.
Challenges
Many scenarios represent a combination of lump sum and annuity cash flow amounts. There are a variety of approaches to calculating the future or present value for such scenarios. Perhaps the safest approach is to diagram the anticipated cash flows and apply logical manipulations.
To illustrate, assume that Markum Real Estate is considering buying an office building. The building will be vacant for two years while it is being renovated. Then, it will produce annual rents of $100,000 at the beginning of each of the next three years. The building will be sold in five years for $700,000. Markum desires to know the present value of the anticipated cash inflows, assuming a 5% annual interest rate.
The rental stream has a present value of $285,941 as of the beginning of Year 3. That value is discounted back to the beginning of Year 1 value ($259,357) by treating it as a lump sum. The sales price is separately discounted to its present value of $548,471. The present value of the rents and sales price are combined to produce the total present value for all cash inflows ($807,828). This type of cash flow manipulation is quite common in calculating present values for many investment decisions.
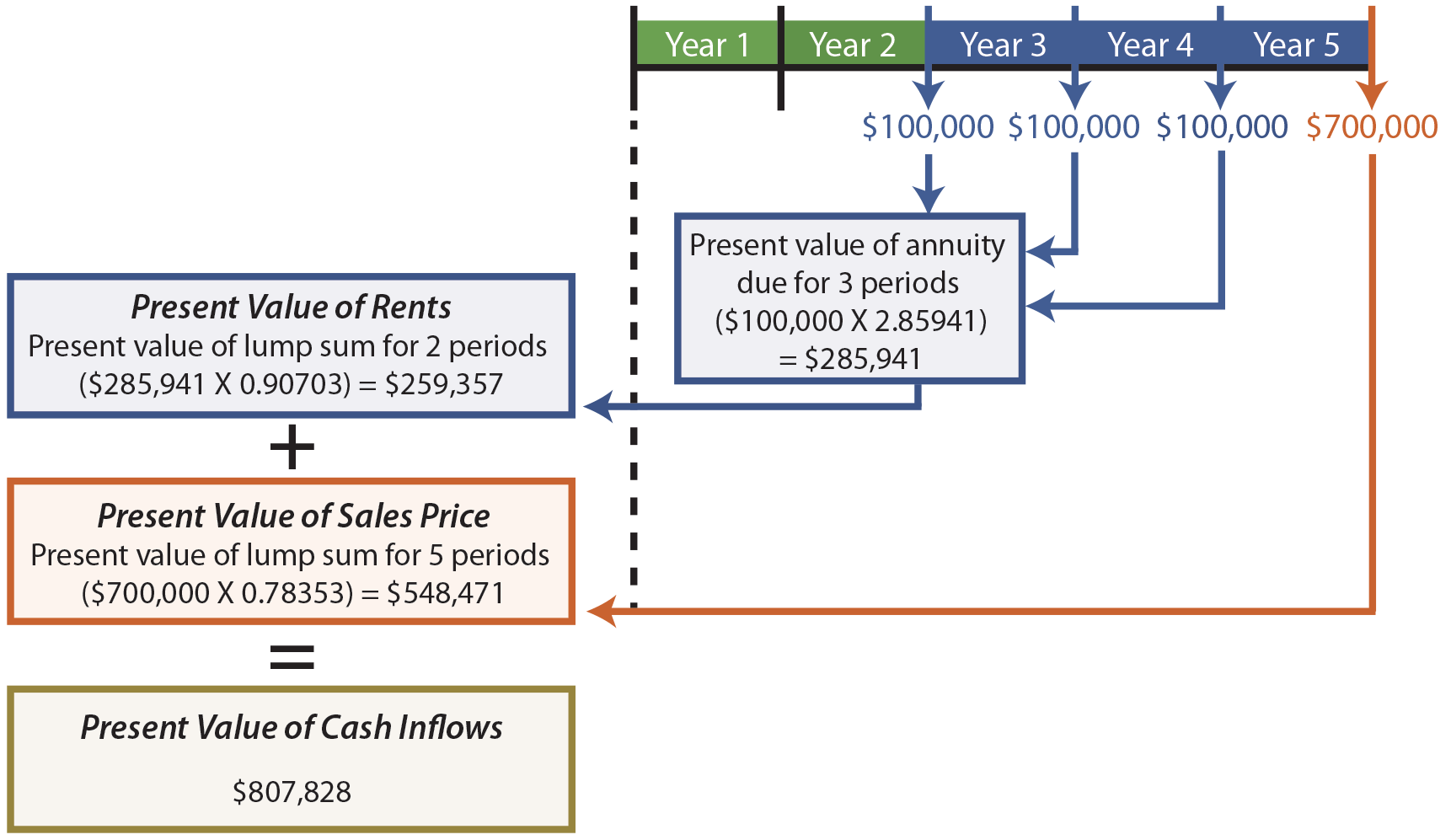
An alternative way to value the rental stream would be to subtract the value for a 2-year annuity from the value for a 5-year annuity (4.54595 – 1.95238 = 2.59357; $100,000 X 2.59357 = $259,357). This result occurs because it assumes a 5-year annuity and backs out the amount relating to the first two years, leaving only the last three years in the resulting present value factor.
| Did you learn? |
|---|
| What is meant by the “time value of money?” |
| Be able to calculate compound interest. |
| Understand the relationship between compound interest and present value. |
| Be able to calculate future value and present value of lump-sum and annuity amounts. |