 Prior chapters illustrate notes payable of short duration. However, borrowers may desire a longer term for a loan. It would be common to find two-, three-, five-year, and even longer term notes. These notes may evidence a “term loan,” where “interest only” is paid during the period of borrowing and the balance of the note is due at maturity. To illustrate, assume that a $10,000, five-year, 8% term note, is issued on October 1, 20X3 :
Prior chapters illustrate notes payable of short duration. However, borrowers may desire a longer term for a loan. It would be common to find two-, three-, five-year, and even longer term notes. These notes may evidence a “term loan,” where “interest only” is paid during the period of borrowing and the balance of the note is due at maturity. To illustrate, assume that a $10,000, five-year, 8% term note, is issued on October 1, 20X3 :

Interest on the note must be accrued each December 31, with payment following on September 30.

The following entry is needed at maturity on September 30, 20X8:

Other Types Of Notes
With the term note illustration, it is easy to calculate interest of $800 per year, and observe the $10,000 balance due at maturity. Other loans may require level payments over their terms, so that the interest and principal are fully paid by the end of the loan. This type of arrangement is commonly used for real estate financing. The payment of the note is usually secured by the property, allowing the lender to take possession for nonpayment. Real estate notes thus secured are called “mortgage notes.” How are payments calculated? The first step is to learn about future value and present value calculations.
Future Value
 Let’s start by thinking about how invested money can grow with interest. What will be the future value of an investment? If $1 is invested for one year, at 10% interest per year, it will grow to $1.10. This is calculated by multiplying the $1 by 10% ($1 X 10% = $0.10) and adding this $0.10 to the original dollar.
Let’s start by thinking about how invested money can grow with interest. What will be the future value of an investment? If $1 is invested for one year, at 10% interest per year, it will grow to $1.10. This is calculated by multiplying the $1 by 10% ($1 X 10% = $0.10) and adding this $0.10 to the original dollar.
And, if the resulting $1.10 is invested for another year at 10%, it will grow to $1.21. That is, $1.10 X 10% = $0.11, which is added to the $1.10 value from the end of the first year. This process will continue year after year. The annual interest each year is larger than the year before because of “compounding.”
Compounding simply means that the investment is growing with accumulated interest and earning interest on previously accrued interest. The contrast to compound interest is simple interest. Simple interest does not provide for compounding, such that $1 invested for two years at 10% would only grow to $1.20.
The preceding observations lead to this compound interest calculation:
(1+i)n
Where “i” is the interest rate per period and “n” is the number of periods
This calculation reveals how much an investment of $1 will grow to after “n” periods. If $1 was invested for 5 years at 6%, then it would grow to about $1.34 [(1.06)5 = 1.33823]. Of course, if $1,000 was invested for 5 years at 6%, it would grow to $1,338.23; this is determined by multiplying the derived factor times the amount invested at the beginning of the 5-year period. This calculation is aptly termed the “future value of a lump sum amount.”
Future value amounts can always be calculated using the preceding formulation. However, spreadsheet software and business calculators frequently include built-in routines to return appropriate values. Another useful tool is a future value table. These tables include values corresponding to various rates and periods. Use a table, spreadsheet, or business calculator to verify the 1.33823 factor for a 5-period, 6% investment. Likewise, determine that $5,000, invested for 10 years, at 4%, will grow to $7,401.20 ($5,000 X 1.48024).
Present Value
Present value is the opposite of future value, as it reveals how much a dollar to be received in the future is worth today. The math is simply the reciprocal of future value calculations:
1/(1+i)n
Where “i” is the interest rate per period and “n” is the number of periods
For example, $1,000 to be received in 5 years, when the interest rate is 7%, is presently worth $712.99 [$1,000 X (1/(1.07)5)]. Stated differently, if $712.99 is invested today at 7%, it will grow to $1,000 in 5 years. Present value amounts are also determinable from spreadsheets, calculators, or tables. Verify that the present value of $50,000 to be received in 8 years at 8% is $27,013.50 ($50,000 X .54027).
Annuities
Streams of level payments (i.e., the same amount each period) occurring on regular intervals are termed annuities. For example, if one invests $1 at the beginning of each year at 5% per annum, after 5 years it would accumulate to $5.80. This can be painstakingly calculated by summing the future value amount associated with each individual payment, as shown in the following calculations.
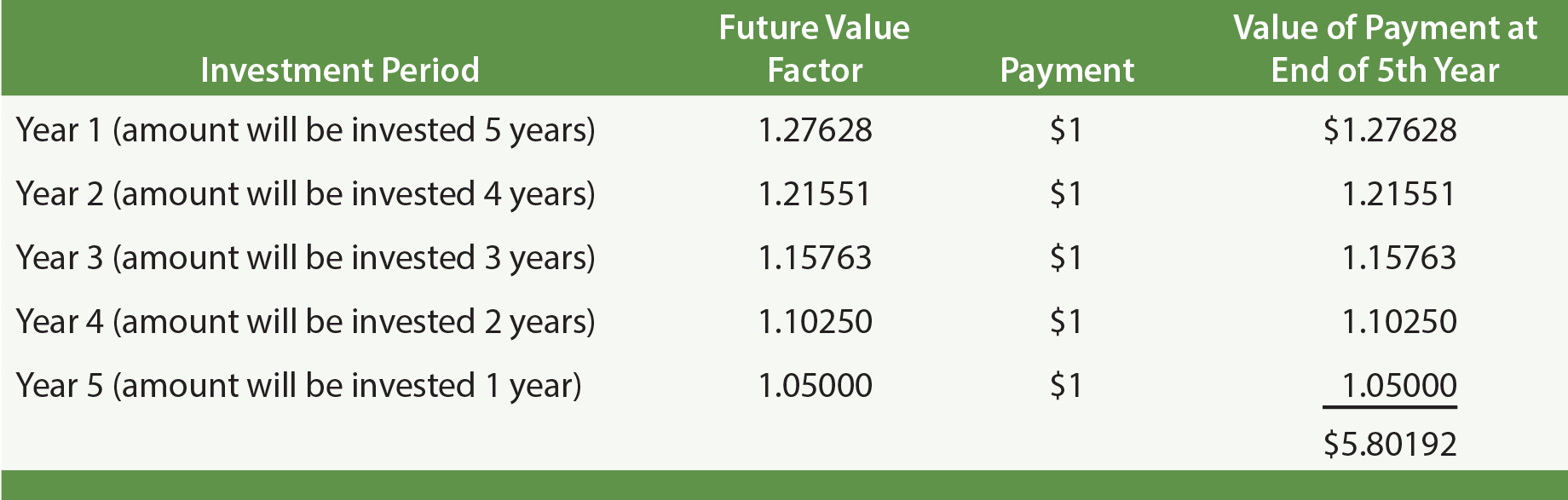
But, it is much easier to use spreadsheets, calculators, or annuity future value tables. The annuity table is simply the summation of individual factors. Verify the “5.80“ factor from the 5% row, 5-year column of a table. These calculations are useful in financial planning. For example, one may wish to have a target amount accumulated by a certain age, such as with a retirement account. These factors help calculate the amount that must be set aside each period to reach the goal.
Conversely, one may be interested in the present value of an annuity which reveals the current worth of a level stream of payments to be received at the end of each period. Use a table, calculator, or spreadsheet to find the present value of $1,000 to be received at the end of each year for 5 years, if the interest rate is 8% per year. The 5-year column, 8% row of the appropriate table shows a factor of 3.99271, indicating that the present value of the annuity is $3,992.71.
Note Payments
How does one compute the payment on a typical loan that involves level periodic payments, with the final payment satisfying the remaining balance due? The answer to this question is found in the present value of annuity calculations. Remember that an annuity involves a stream of level payments, just like many loans. The payments on a loan are a series of level payments that cover both the principal and interest. The present value of those payments is the amount borrowed, in essence “discounting” out the interest component. This concept may still be a bit abstract, but can be further clarified mathematically with some equations:
Present Value of Annuity = Payments X Annuity Present Value Factor
A loan that is paid off with a series of equal payments is also an annuity, therefore:
Loan Amount = Payments X Annuity Present Value Factor
Thus, to determine the annual payment to satisfy a $100,000, 5-year loan at 6% per annum:
$100,000 = Payment X 4.21236 (from table)
Payment = $100,000 / 4.21236 = $23,739.64
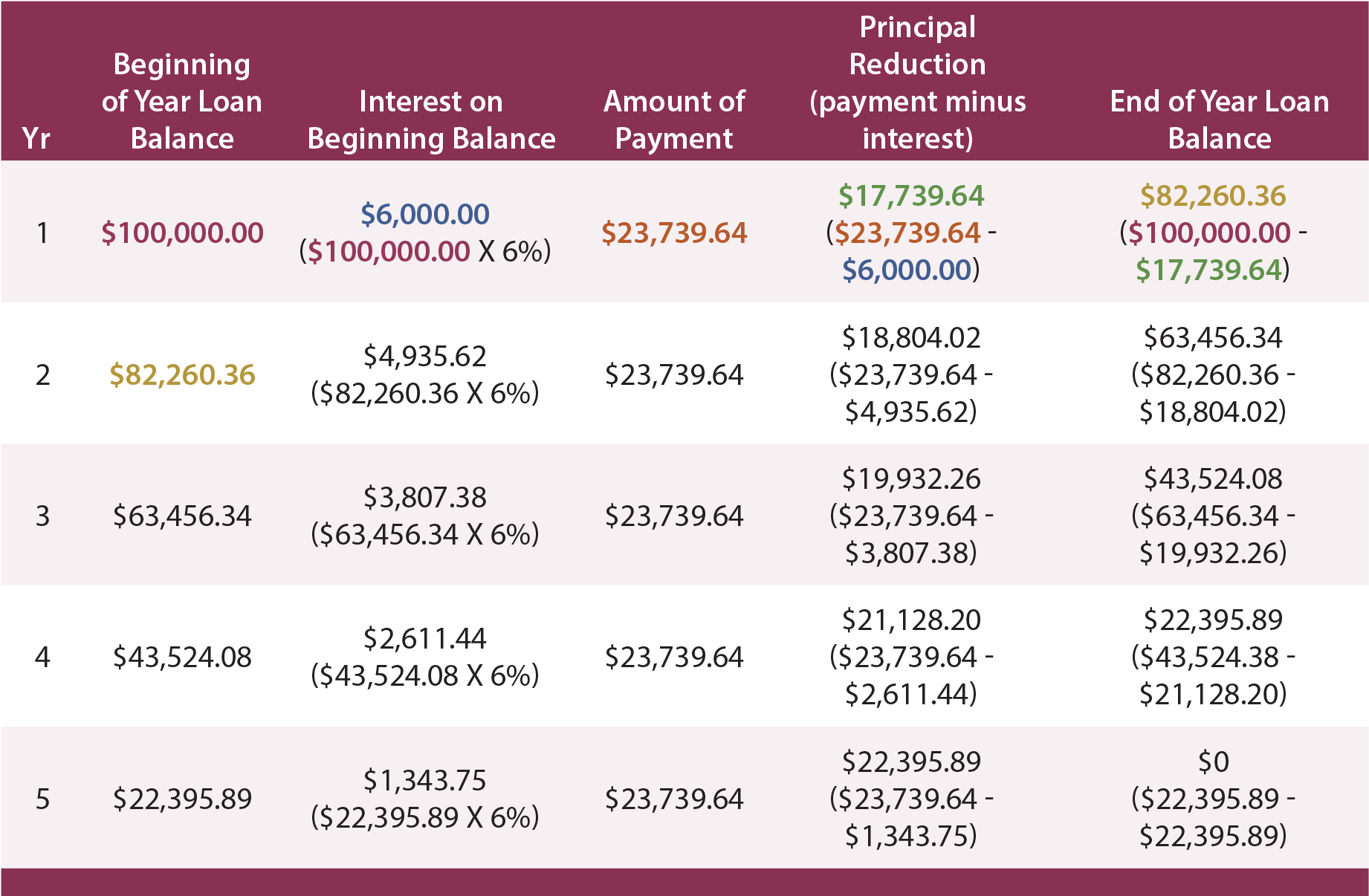
The five payments of $23,739.64 will exactly pay off the $100,000 loan plus all interest at a 6% annual rate. Simply stated, the payments on a loan are just the loan amount divided by the appropriate present value factor. To fully prove this point, look at the following typical loan amortization table. This table shows how each payment is applied to first satisfy the accumulated interest for the period, and then reduce the principal. Note that the final payment will extinguish any remaining principal.
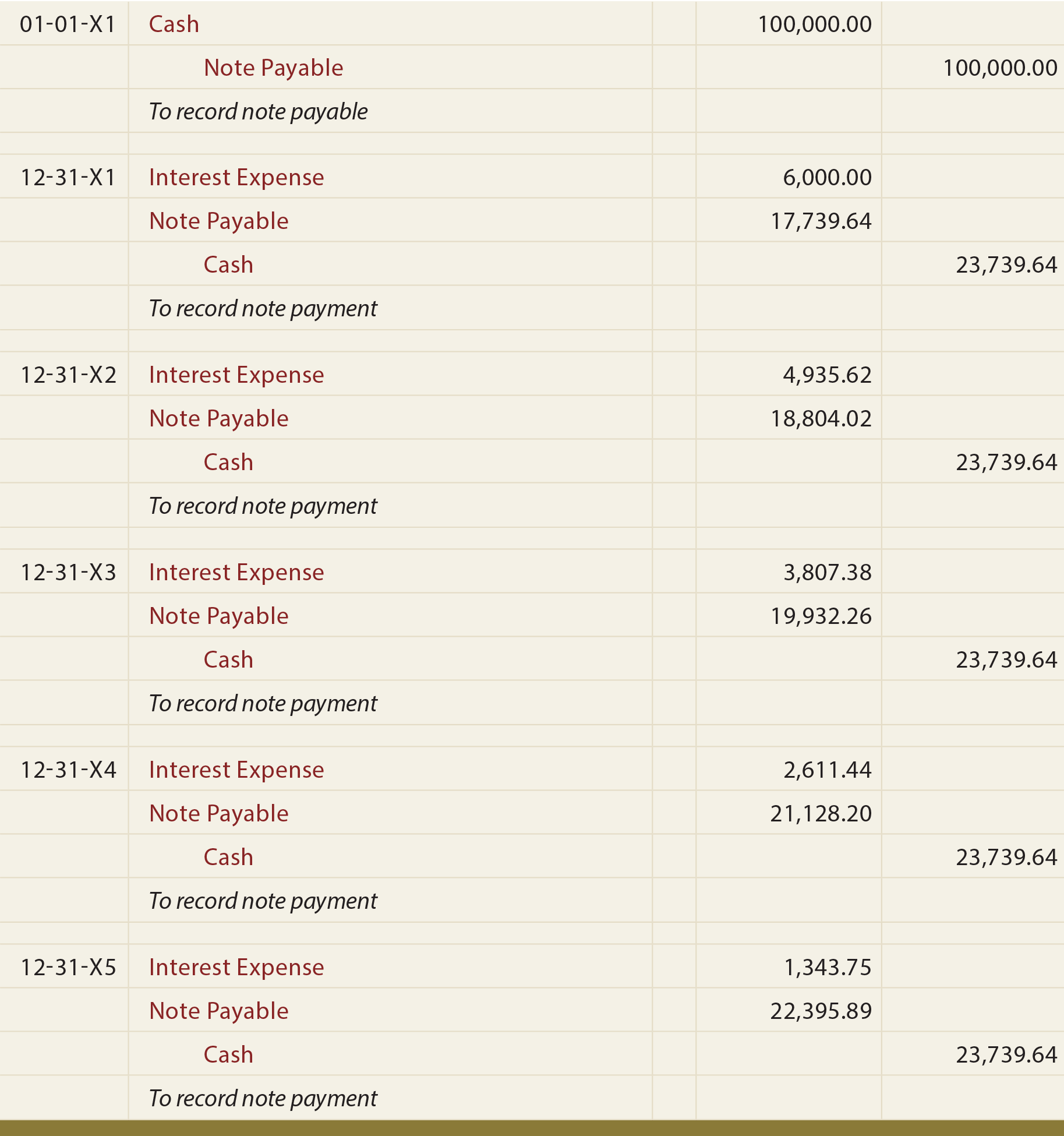
The journal entries associated with the preceding loan would flow as follows:
A Few Final Comments On Future And Present Value
Note that some scenarios may involve payments at the beginning of each period, while other scenarios might require end-of-period payments. Later chapters of this book include additional future and present value calculations for alternatively timed payment streams (e.g., present value of an annuity with payments at the beginning of each period).
Also note that payments may occur on other than an annual basis. For example, a $10,000, 8% per annum loan may involve quarterly payments over two years. The quarterly payment would be $1,365.10 ($10,000/7.32548). The 7.32548 present value factor is reflective of 8 periods (4 quarters per year for 2 years) and 2% interest per period (8% per annum divided by 4 quarters per year). This type of modification applies to annuities and lump-sum amounts. For example, the present value of $1 invested for 5 years at 10% compounded semiannually can be determined by referring to the 5% row, 10-period factor.
As previously noted, spreadsheet software normally includes functions to help with fundamental present value, future value, and payment calculations. Following is a screen shot of one such routine:
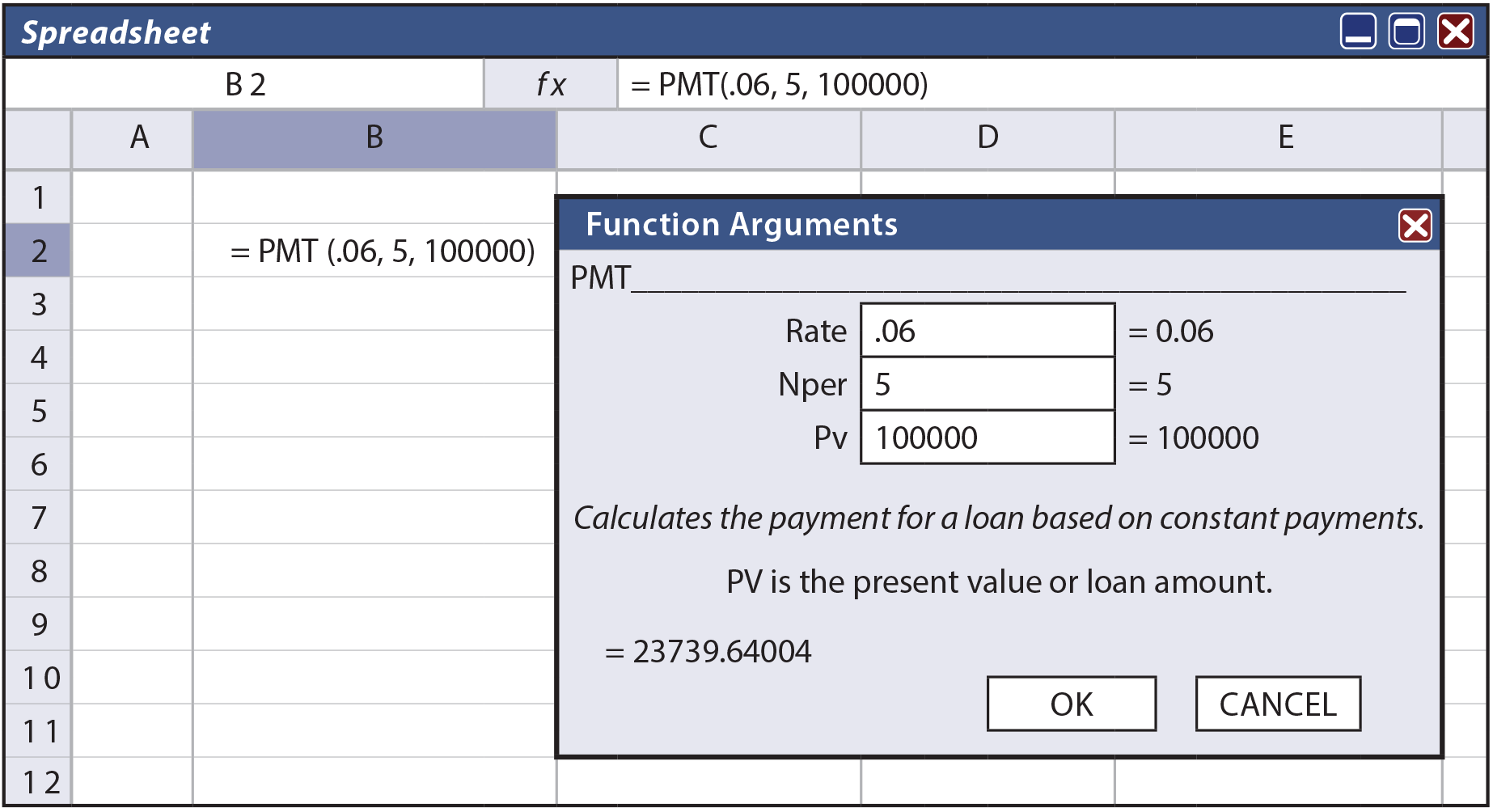
| Did you learn? |
|---|
| Be able to account for a simple term note payable. |
| Understand compound interest concepts and calculations. |
| Define “future value,” and know the computations and how to use future value tables (for lump sum and annuity situations). |
| Define “present value,” and know the computations and how to use present value tables (for lump sum and annuity situations). |
| Calculate and account for amounts related to notes payable that include level payments of principal and interest over their life. |
| Know that electronic spreadsheets frequently include functions that can be used to calculate note payments. |
